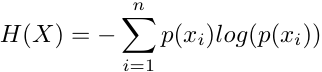Organodynamics	Grant Holland, Apr 25, 2014
Slide: Organodynamics and Information Theory	Nav Refs Top Bottom Previous Next 90m 90m 45m 45m 25m 25m
Recall what the sample points of our organodynamics probability space (OSS) look like: - Each sample point is a topology (extended)… - Where each open set has a relation paired to it. The OSS, itself, is the set of all such extended topologies. Note: There is no semantically useful assignment of real numbers to these sample points (topologies)! Therefore, the sample space of our organodynamic probability space (OPS) is very complex – yet has no meaningful mapping to the real numbers.	No meaningful mapping of sample points in an OSS to real numbers This means that the statistical mean of an OPD is undefined! Because the value function v(X) is undefined! Mean μ = E[v(X)] This also means that the variance of an OPD is undefined! Also because v(X) is undefined! Variance μ2 = E[v(X)] - μ]^2 Also undefined are the skewness, kurtosis, and all other central moments of an OPD: μn = E[v(X)] - μ]^n
Mathematical Statistics No moment or central moment of an OPD exists! Because no meaningful value function exists on an OPD. It can be reasonably suggested that moments and central moments are the central devices of mathematical statistics. Thus, mathematical statistics is not useful to characterized chance variation (random fluctuation) in organodynamics.	Information theory Fortunately, entropic functionals do exist for organodynamics, because they only require probabilities – no value functions are required: Entropy It is reasonable to define Information Theory as the study of entropic functionals.

Notes: