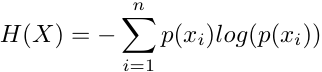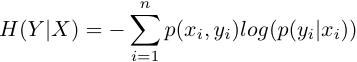Organodynamics	Grant Holland, Apr 25, 2014
Slide: Two ways to characterize chance variation	Nav Refs Top Bottom Previous Next 90m 90m 45m 45m 25m 25m
First way: Moments and central moments - A set of functionals that measure chance variation. - Maps a probability space to a series of real numbers - Measures degree of variation about a center Examples: Mean, variance, skewness, kurtosis, … The calculation of these moments require the prior definition of two real-valued functions on the sample space X of the probability space (X, F, p): 1. Probability assignment p(X) – already a part of the probability space 2. Value function v(X) – an association of each x in X to some real number. v(X) is NOT part of the probability space, but must be defined external to it.	Some moments and central moments Mean μ = E[v(X)] Variance μ2 = E[v(X)] - μ]^2 Skewness μ3 = E[v(X)] - μ]^3 Kurtosis μ4 = E[v(X)] - μ]^4 n^th central moment μn = E[v(X)] - μ]^n Note: Both probabilities and a value function is required for these.
Second way: Entropic functionals - A set of functionals that measure chance variation - Maps a probability space to a series of real numbers - Measures degree of choice and uncertainty Examples: Entropy, conditional entropy, relative entropy, mutual information, entropy rate The calculation of these entropic functionals does not require a value function v(X) on the sample space. Only probabilities: Probability assignment p(X) – already a part of the probability space	Some entropic functionals No value function v(X) is required or used. Nothing outside the definition of probability space is used. Entropy Conditional entropy Relative entropy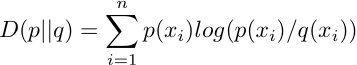

Notes: