Organodynamics	Grant Holland, Apr 25, 2014
Slide: Stochastic Dependence and Predictability	Nav Refs Top Bottom Previous Next 90m 90m 45m 45m 25m 25m
Sometimes, knowing the outcome of one time step (in a stochastic process) provides extra information that helps to more accurately predict the outcome of the next time step. This is accomplished by providing a distinct probability distribution to each possible outcome of the current time step. This situation is called the “probability of Y given X”, or “p(Y|X)”; and is referred to as conditional probability. This is represented by a transition matrix, which is derived from the joint distribution of variables X and Y. Conditional probability describes when two chance variables are stochastically dependent. If all the rows of the transition matrix are the same, then the two variables are statistically independent. The more different are the rows of the transition matrix, the more stochastically dependent they are.	The more two chance variables are stochastically dependent, the more predictable is their joint distribution. Therefore, predictability increases as the degree of stochastic dependence increases. Thus, the long-run predictability of a stochastic process increases as the mutual dependence of its time steps increases. This is the key to measuring the stability of a stochastic process.
Mutual information, I(X;Y), is an entropic functional that measures the degree of stochastic dependence between two chance variables. 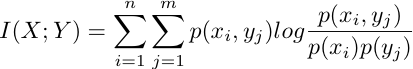Entropy rate is an entropic functional that characterizes the long-run uncertainty of a stochastic process.	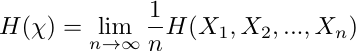Thus, the entropic functionals of information theory can describe the stability/instability, or other interpretations of uncertainty in stochastic processes. Organodynamic applications must find a stochastic dependency, or influence, between outcomes of consecutive time steps in order to get constrained behavior. When that is found, then a stochastic dynamics is achieved.

Notes: